The Distribution of F-ratios

The F-Ratio:

The heart of ANOVA is analyzing the total variability into these two components, the mean square between and mean square within.

Once we have analyzed the total variability into its two basic components we simply compare them. The comparison is made by computing the F-ratio. For independent-measures ANOVA the F-ratio has the following structure:

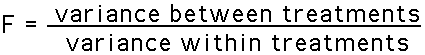
or, using the vocabulary of ANOVA,

Characteristics of the F-ratio

1. The numerator and denominator of the ratio measure exactly the same variance when the null hypothesis is true. Thus: when Ho is true, F is about 1.00.
2. F-ratios are always positive, because the F-ratio is a ratio of two variances, and variances are always positive.

Given these two factors, we can sketch the distribution of F-ratios. The distribution piles up around 1.00, cuts off at zero, and tapers off to the right.

Degrees of Freedom:

Note that the exact shape depends on the degrees of freedom of the two variances. We have two separate degrees of freedom, one for the numerator (sum of squares between) and the other for the denominator (sum of squares within). They depend on the number of groups and the total number of observations. The exact number of degrees of freedom follows these two formulas (k is the number of groups, N is the total number of observations):

Two F Distributions:

Here are two examples of F distributions. They differ in the degrees of freedom:

1. For the data about learning under different termperature condtions (discussed above), the df(between)=3-1=2, and the df(within)=15-3=12. We can look up the critical value of F (.05) and find that it is 3.88. The observed F=11.28, so we reject the null hypothesis. The F-ratio distribution is:
   

2. For data where df=5,30 (6 groups, 36 observations), the F-ratio distribution is:
   

---