Two-Way ANOVA is used in research situations in which there are two independent (classification) variables - two-factor experiments, in the Gravetter and Wallnau terminology.

Example

An experiment is designed to investigate change in systolic blood pressure after administering one of four different drugs to patients with one of three different blood diseases. These data are from Afifi and Azen (1972), and are cited in Kutnet (1974). They are used as an example of 2-way ANOVA in SAS, BMDP and SYSTAT. You can download the ViSta Data. You can also download the Eysenck Data

In these data:

1. the independent (classification) variables are drug and disease.
2. the dependent (response) variable is systolic blood pressure.

This is a two-way experiment whose design is called a "three-by-four factorial design".

Here are the data:

Systolic Blood Pressure
.	Disease A	Disease B	Disease C
Drug 1	42 44 36 13 19 22	33 26 33 21	31 -3 25 25 24
Drug 2	28 23 34 42 13	34 33 31 36	3 26 28 32 4 16
Drug 3	1 29 19	11 9 7 1 -6	21 1 9 3
Drug 4	24 9 22 -2 15	27 12 12 -5 16 15	22 7 25 5 12

For ViSta these data are entered as a multivariate matrix with three variables: One of the variables is the response (dependent) variable, which is change in blood pressure. The other two variables are the classification (independent) variables, Drug and Disease.

Here is how the first few values would be entered:

Pressure	Drug	Disease
Numeric	Category	Category
42	Drug1	DiseaseA
44	Drug1	DiseaseA
36	Drug1	DiseaseA
13	Drug1	DiseaseA
19	Drug1	DiseaseA
22	Drug1	DiseaseA
33	Drug1	DiseaseB
26	Drug1	DiseaseB
33	Drug1	DiseaseB
...continued...

---

Factorial Design

Definition: An experimental design in which every level of every way of the design is paired with every level of every other way of the design is called a Factorial Design. Such a design includes all combinations of the levels of the independent variables.

• Factors: The ways of the design are often called factors.
• Levels: A specific value of a factor.
• Cells: A cell of a factorial design is a specific combination of a particular level of each factor of the design.

Advantages: Factorial designs have several important advantages over one-way designs.

1. Generalizability:
   They allow greater generalizability of results. If we only ran the blood pressure study with one disease we wouldn't know whether the results applied to other diseases. Doing the study with three diseases allows us to generalize across at least some diseases.
2. Interaction:
   They allow us to look at interaction of the variables. We can ask whether the effect of the drugs is independent of the disease (i.e., is the same for the diseases) or whether there is an interaction (i.e., they work differently for different diseases). In two-way designs we can look at two-way interactions.
3. Economy:
   We can have fewer subjects and still have a powerful experiment, since we can look at the effect of one factor (Drug or Disease) averaged over the levels of the other factor.

N-Way Factorial Designs.
We can have more than just two ways of the design. For example, the drug study could be performed at two different hospitals, making for a 3x4x2 factorial design.

• In three-way designs we can look at every pair of two-way interactions as well as the three-way interaction, an advantage.
• In higher-way designs we can look at very many interaction terms, but they become hard to understand.
• ViSta can only look at two-way interactions.

Balanced/Unbalanced Factorial Designs.
A balanced factorial design is one that has the same number of observations in every cell. Unbalanced designs do not have the same number. The data above are unbalanced.

• The calculations for unbalanced designs are more complex and the interpretation can be very unclear.
• It is best to avoid these unbalanced data, but in survey research such analyses are common.
• ViSta can analyze them.

Complete/Incomplete Factorial Designs.
A complete factorial design is one for which every cell has some data.

• Incomplete designs, in which some cells have missing data, are very difficult to analyze, and are difficult to interpret.
• These designs should be avoided.
• ViSta cannot analyze incomplete data.

---

Analysis Results

Here is the report produced by ViSta's analysis of the blood-preasure data:

Hypotheses

The two-way ANOVA for a factorial design provides three separate hypothesis tests in one analysis. These hypothese are like those in one-way ANOVA. They are non-directional.

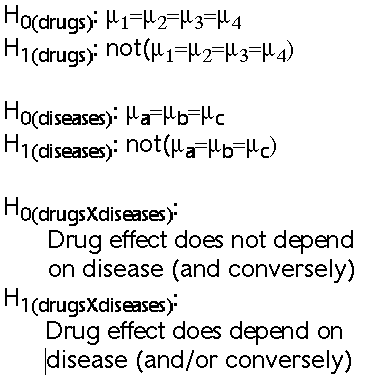
F-Tests

• Each F-test is based on its own F-Ratio. Each F-Ratio has the same basic structure given for one-way ANOVA (variance of the sample means divided by error variance):
  
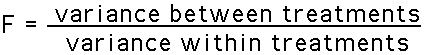
• Each F-Ratio is evaluated for significance in just the same way we saw for one-way ANOVA.

Systolic Blood Pressure Example

For our example two-way ANOVA allows the researcher to construct F-Tests that reveal:

• the significance of the differences between the four drugs
• the significance of the differences between the three diseases
• the significance of any other differences that may result from unique combinations of a specific drug and a specific disease (for example, drug 1 may be particularly effective with disease B).

Main Effects:

The mean differences among the levels of one factor are called the main effects. In our example we have two main effects: The Drug effect and the Disease effect.

In our example the design of the research study is represented as a table. The Drug factor determines the rows and the Disease factor the columns. The differences among the row means describes the main effect for the Drug factor. Similarly, the differences among the column means describes the main effect for the Disease factor.

Note that the differences among the means describes the main effects. These differences are the basis of the F-test. It tests whether the differences are statistically significant.

There is a seperate set of hypothesis for each main effect, and a separate F-test for each main effect. Each test has it's own p-level.

Interactions:

In addition to evaluating the significance of the differences in means for each main effect, two-way ANOVA allows you to evaluate differences in means that may result from unique combinations of the two main factors.

There is an interaction between two factors if the effect of one factor depends on the levels of the other factor.

There is a seperate hypothesis for the interaction effect, and a separate F-test for the interaction effect. The test has it's own p-level.

For this example we conclude

• There is a significant effect for Drugs: They do not all have the same effect on the patients, regardless of disease. The effect of the drug depends on the patient's disease.
• There is no effect for Diseases: The drugs have the same effects on patients regardless of their disease.
• There is no significant interaction effect.

And here is the visualization.

• The diamond plot that is shown shows that drugs 1 and 2 have a greater effect on change in systolic blood preasure than drugs 3 and 4. Other boxplots (seen by clicking sources in the source window) show no effects for disease or interaction.
• The partial regression plot that is shown shows that the effect for drugs is significant at the .05 level, since the confidence envelope crosses the horizontal line. Other partial regression plots show no effect.

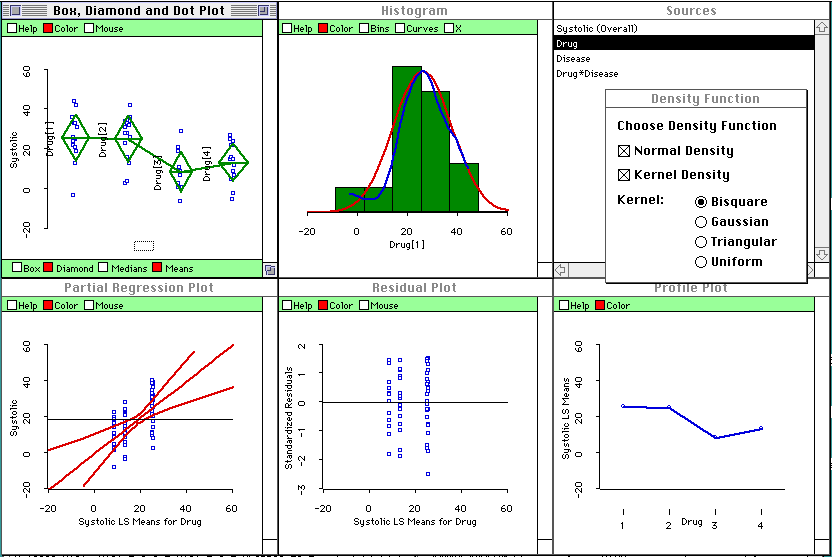
Rather than show all the results here, we turn to the ViSta Data Applet for these data.

---